3.1 KiB
#start of lec 35
last problem of the course which we will finish today.
\frac{ \partial^2 u }{ \partial t^2 }=\frac{ \partial^2 u }{ \partial x^2 }+tx, 0\leq x\leq \pi t>0
thats a driven wave equation. tx is the source term.
u(0,t)=u(\pi,t)=0 \quad t>0
u(x,0)=\sin(x) \quad 0\leq x\leq \pi
\frac{ \partial u }{ \partial t }(x,0)=5\sin(2x)-3\sin(5x)\quad 0\leq x\leq \pi
if any of the boundary conditions are non zero, then we have to split(?) into X and T.
in this case there's a \sin(x) term so its a nonhomogenous equation (?)
when tx wasn't there in last problem we had the solution:
u(t,x)=\sum_{n=1}^\infty \underbrace{ (a_{n}\cos(nt)+b_{n}\sin(nt)) }_{ u_{n}(t) }\sin(nt) notice L=\pi
if we expand tx:
tx=\sum_{n=1}^\infty h_{n}\sin(nx) (this is called a formal expansion, the two arent exactly equal due to the discontinuouity in tx.)
h_{n}=\frac{2}{\pi}\int _{0} ^\pi tx\sin(nx)\, dx
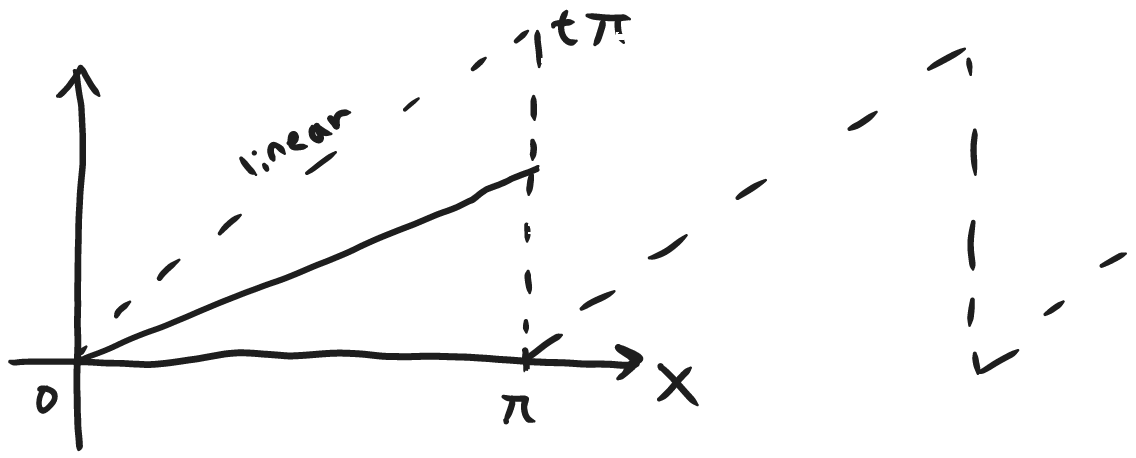
continuous between 0 and pi but on the edge ponts, the foureir sin series will converge to the midpoint of the two edge points.
h_{n}=\frac{2t}{\pi}\int _{0}^\pi x\sin(nx)\, dx=- \frac{2t}{\pi n}\left( x\cos(nx)|_{0}^\pi-\int _{0}^\pi \cancel{ \cos(nx) }\, dx \right)
h_{n(t)}=\frac{2t}{n}(-1)^{n+1}
h(x,t)=tx=\sum_{n=1}^\infty h_{n}\sin(nx)=\sum_{n=1}^\infty \frac{2t}{n}(-1)^{n+1}\sin(nx)
\frac{ \partial^2 u }{ \partial t^2 }=\sum_{n=1}^\infty u_{n}''(t)\sin(nx)
\frac{ \partial^2 u }{ \partial x^2 }=\sum_{n=1}^\infty -u_{n}(t)n^2\sin(nx)
\sum_{n=1}^\infty \underbrace{ \left( u_{n}''+n^2u_{n}+\frac{2t}{n}(-1)^n \right) }_{ =0 }\sin(nx)=0
u''_{n}+n^2u_{n}=\frac{2}{n}(-1)^{n+1}t, \quad n=1,2,\dots
use #mouc (or laplace, but that'll take much longer.)
characteristic eq:
r^2+n^2=0
r_{1,2}=\pm in
u_{n}^h(t)=a_{n}\cos(nt)+b_{n}\sin(nt)
u_{n}^p(t)=At+B
B=0 because there's no constant term on the RHS
A=\frac{2(-1)^{n+1}}{n^3}
u_{n}(t)=a_{n}\cos(nt)+b_{n}\sin(nt)+\frac{2(-1)^{n+1}}{n^3}t
u(x,t)=\sum_{n=1}^\infty(a_{n}\cos(nt)+b_{n}\sin(nt)+\frac{2(-1)^{n+1}}{n^3}t)\sin(nx)
This is the last problem I'll be solving in my career. This is the last time he's teaching math 201 :( or any course for that matter.
u(x,0)=\sum_{n=1}^\infty a_{n}\sin(nx)=\sin(x)
a_{1}=1, \quad a_{k}=0, \quad k=2,3,\dots
\frac{ \partial u }{ \partial t }(x,0)=\sum_{n=1}^\infty\left( b_{n}n+\frac{2(-1)^{n+1}}{n^3} \right)\sin(nx)=5\sin(2x)-3\sin(5x)
coefficients =0 if n\ne_{2},5
\implies b_{n}=\frac{2}{n^4}(-1)^n, \quad n\ne_{2},5
b_{2}=\frac{5}{2}+\frac{2(-1)^2}{2^4}
b_{5}=-\frac{3}{5}+\frac{2(-1)^5}{5^4}
u(x,t)=\cos(t)\sin(x)+\frac{5}{2}\sin(2t)\sin(2x)-\frac{3}{5}\sin(5t)\sin(5x)+2\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^3}\left( t-\frac{\sin(nt)}{n} \right)\sin(nx)
finished the solution. Man I got teary eyed from this lecture.
#end of lec 35
#start of lec 36
What do you guys wanna do? Questions or summary of the course?
Okay we do summary.
Summary of second half of Math 201
(available on eclass)
Laplace transforms:
Definition of laplace,
Properties (4 important ones)
...
#end of lec 36
#end of Math 201. Congratulations!