4.7 KiB
#start of lec 19 This lecture we will learn about periodic functions, specifically, non-sinusoidal periodic functions.
Periodic function
#periodic
Definition:
f is periodic with period T \quad (T>0) if:
f(t)=f(t+T), \quad \forall\ t\in \mathbb{R}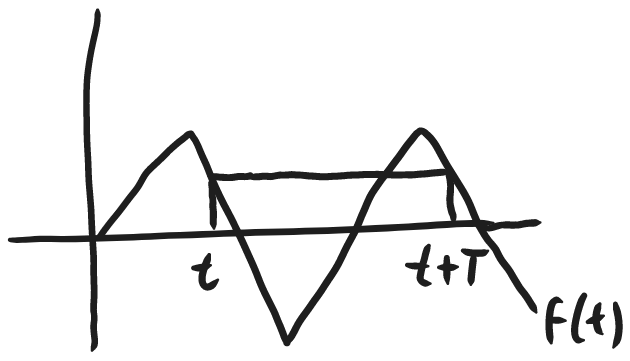
We will now compute laplace transforms of these periodic functions. Computing DE's containing these periodic functions using something like #voparam would not be easy.
Let's try taking the laplace of a periodic function f(t):
If we take the windowed version of the function (one period, where everywhere else is 0, ie:)
f_{T}(t)=\begin{cases}f(t)\ ,\ & 0\leq t\leq T \\0\ ,\ & \text{otherwise}\end{cases}
we can "glue together" many of these windows together to rebuild our f(t), like this:
f(t)=f_{T}(t)+f_{T}(t-T)+f_{T}(t-2T)+\dots
We can add some unit step functions strategically such that it doesn't change the overall expression:
f(t)=f_{T}(t)+f_{T}(t-T)u(t-T)+f_{T}(t-2T)u(t-2T)+\dots
hit it with the LT!
\mathcal{L}\{f\}=\mathcal{L}\{f_{T}\}+\mathcal{L}\{f_{T}(t-T)u(t-T)\}+\dots
recall the formula from last lec: \mathcal{L}\{u(t-a)f(t-a)\}=e^{-as}F(s)
then:
\mathcal{L}\{f\}=\mathcal{L}\{f_{T}\}(1+e^{-Ts}+e^{-2Ts}+e^{-3Ts}+\dots)
\mathcal{L}\{f\}=\mathcal{L}\{f_{T}\}(1+e^{-Ts}+(e^{-Ts})^{2}+(e^{-Ts})^{3}+\dots)
This is a geometric series! 1+r+r^2+\dots
Geometric series are convergent when |r|<1
and equal to: \frac{1}{1-r}
in this case, r=e^{-Ts}
so:
\mathcal{L}\{f\}=\mathcal{L}\{f_{T}\} \frac{1}{1-e^{-Ts}}handy formula! ^ will be used again.
#ex
Imagine another function: (image is of a square wave with a period of 2a, oscillates between 1 and 0, starts at 1 when t=0.)
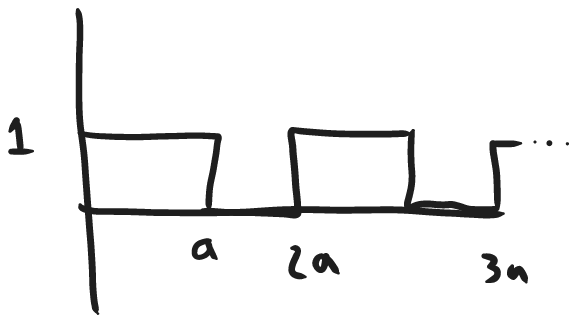Let's compute its LT:
\mathcal{L}\{f\}=\mathcal{L}\{f_{2a}\} \frac{1}{1-e^{-2as}}
f_{2a}=u(t)-u(t-a) (this is the first period piece)
\implies \mathcal{L}\{f_{2a}\}=\mathcal{L}\{u(t)\}-\mathcal{L}\{u(t-a)\}=\frac{1}{s}- \frac{e^{-as}}{s}
plug back in:
\mathcal{L}\{f\}=\mathcal{L}\{f_{2a}\} \frac{1}{1-e^{-2as}}=\frac{1}{s}\cancel{ (1-e^{-as}) } \frac{1}{\cancel{ (1-e^{-as}) }(1+e^{-as})}
\mathcal{L}\{f\}=\frac{1}{s(1+e^{-as})}#ex #IVP #periodic #second_order_nonhomogenous #LT #partial_fractions
Solve for y(t) in the following second order periodic equation:
y''+3y'+2y=f(t) \qquad y(0)=y'(0)=0 \quad a=1Hit it with the LT!
s^2Y+3sY+2Y=\mathcal{L}\{f\}= \frac{1}{s(1+e^{-1s})}
(s+1)(s+2)Y= \frac{1}{s(1+e^{-1s})}
Y(s)=\frac{1}{s(s+1)(s+2)} \frac{1}{1+e^{-s}}
What property can we use to find the inverse of that?
psst. We can use
\mathcal{L}\{y\}=\mathcal{L}\{y_{T}\} \frac{1}{1-e^{-Ts}};)
Y(s)=Y_{T}(s) \frac{1}{1+e^{-s}} <- But this is not true! because:
That second term has a 1+e^{-Ts} term in the denominator, it doesn't match up in the formula. There is a fix, peep this:
Y(s)=Y_{T}(s) \frac{1-e^{-s}}{(1+e^{-s})(1-e^{-s})}
Y(s)=Y_{T}(s) \frac{1-e^{-s}}{1-e^{-2s}} <- We are rather lucky, the 2 in the denominator matches T, the period of our function.
We can tuck away the numerator into Y_{T}(s) (this does redefine Y_{T} to the correct expression, and the equation below is now true.)
Y(s)=\underbrace{ \frac{1-e^{-s}}{s(s+1)(s+2)} }_{ Y_{T}(s) } \frac{1}{1-e^{-2s}}
Our equation is now in the correct form. We can now calculate the inverse of Y_{T}(s)
Split up Y_{T}(s) :
Y(s)= \underbrace{ (\frac{1}{s(s+1)(s+2)} }_{ F_{1}(s) }-\underbrace{ \frac{e^{-s}}{s(s+1)(s+2)} )}_{F_{2}(s) } \frac{1}{1-e^{-2s}}
We can use partial fractions for the first term and
\mathcal{L}\{u(t-a)f_{1}(t-a)\}=e^{-as}F_{1}(s) for the second term. (Where a=1)
Using partial fractions:
\frac{1}{s(s+1)(s+2)}=\frac{A}{s}+\frac{B}{s+1}+\frac{C}{s+2}
A(s+1)(s+2)+Bs(s+2)+Cs(s+1)=(A+B+C)s^2+(3A+2B+C)s+2A=1
2A=1\implies A=\frac{1}{2}
\frac{3}{2}+2B+C=0
\frac{1}{2}+B+C=0
subtract the two equations.
1+B=0\implies B=-1
\implies C=\frac{1}{2}
\mathcal{L}^{-1}\{F_{1}\}=\mathcal{L}^{-1}\{\frac{1}{2} \frac{1}{s}-\frac{1}{s+1}+\frac{1}{2} \frac{1}{s+2}\}
\mathcal{L}^{-1}\{F_{1}\}=f_{1}(t)=\frac{1}{2}-e^{-t}+\frac{1}{2}e^{-2t}
Second term, F_{2}(s), use: \mathcal{L}\{u(t-a)f_{1}(t-a)\}=e^{-as}F_{1}(s)=F_{2}(s)
f_{2}(t)=u(t-1)(\frac{1}{2}-e^{-(t-1)}+\frac{1}{2}e^{-2(t-1)})
recombine the two parts:
Y_{T}=F_{1}-F_{2}
\mathcal{L}^{-1}\{Y_{T}\}=\mathcal{L}^{-1}\{F_{1}\}-\mathcal{L}^{-1}\{F_{2}\}
y_{T}(t)=f_{1}(t)-f_{2}(t)
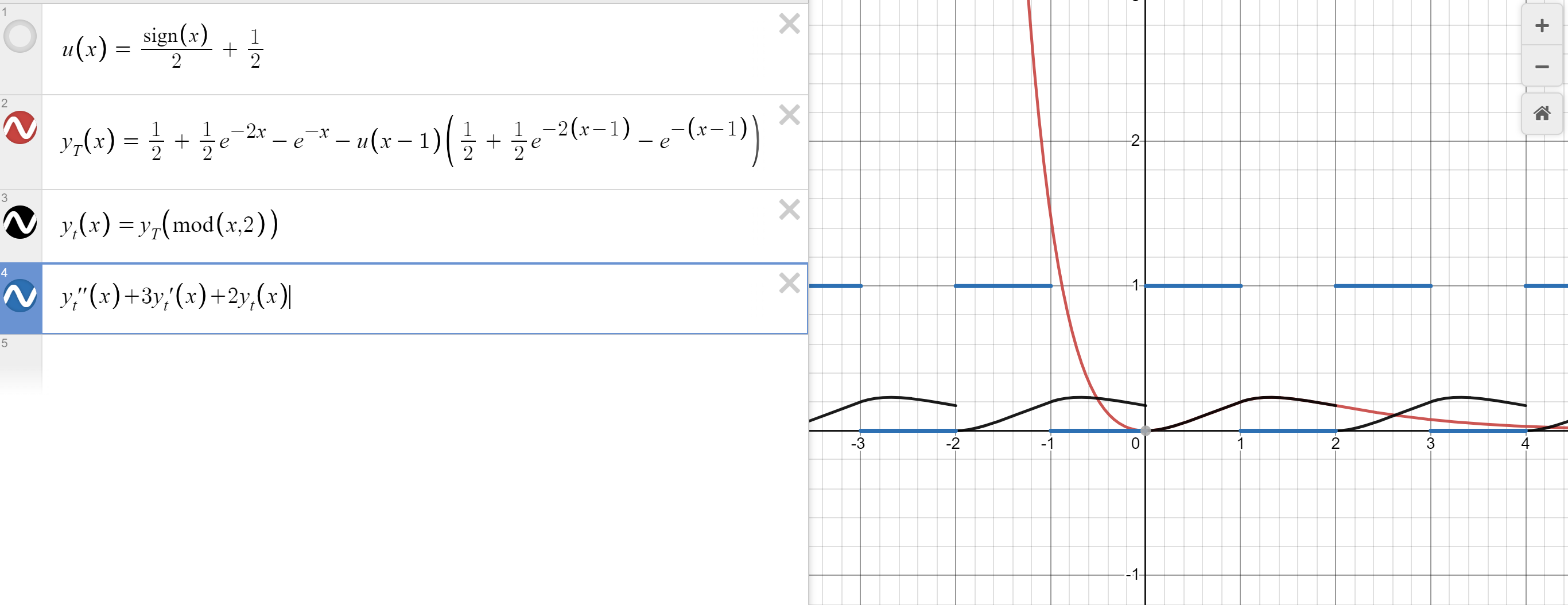
y(t) is a periodic function, with period of T=2
It's windowed form, y_{T}, is:
y_{T}(t)=\frac{1}{2}+\frac{1}{2}e^{-2t}-e^{-t}-u(t-1)(\frac{1}{2}-e^{-(t-1)}+\frac{1}{2}e^{-2(t-1)})Peep da plot!
