MATH201/content/Fourier Series (lec 28-29).md

#fourier Remember the heat flow equation? We obtained that it's solution could be expressed in the form:

\sum_{n=1}^\infty c_{n}\sin\left( \frac{n\pi x}{L} \right)\quad\text{for}\quad0\leq x\leq L

But what is c_{n}? They are the coefficients of a Fourier transform. We want to develop a way to compute them. Let's derive how to compute the coefficients of a Fourier transform. (feel free to skip to the end) f(x)=\sum_{n=1}^\infty b_{n}\sin\left( \frac{n\pi x}{L} \right) where L is length of the rod

This is a Fourier series: it's a more general form of what we have above. f(x)=\frac{a_{0}}{2}+\sum_{n=1}^\infty\left( a_{n}\cos\left( \frac{n\pi x}{L} \right) + b_{n}\sin\left( \frac{n\pi x}{L}\right) \right) x \in [-L,L] It converges to f(x) almost everywhere (convergence will be discussed below) Has a lot of benefits over Taylor series. f(x) doesn't have to be infinitely differentiable (analytic) f(x) can even have jump discontinuities Let's assume the equation is true when x \in [-L,L] Integrate both sides, it will tell us the DC offset: \int _{-L} ^L f(x) \, dx=\int _{-L}^L \frac{a_{0}}{2} \, dx+\int _{-L}^L (\text{put summation here}) \, dx \int _{-L}^L \cos\left( \frac{n\pi x}{L} \right) \, dx=\frac{L}{n\pi}\sin\left( \frac{n\pi x}{L} \right)|_{-L}^L=0 same for \int _{-L}^L \sin\left( \frac{n\pi x}{L} \right)\, dx=0 (it equals 0) so \int _{-L} ^L f(x) \, dx=\int _{-L}^L \frac{a_{0}}{2} \, dx+\int _{-L}^L0 \, dx \int _{-L} ^L f(x) \, dx=a_{0}L a_{0}=\frac{1}{L}\int _{-L}^{L} f(x) \, dx Now let's multiply both sides by \cos\left( \frac{m\pi x}{L} \right) and integrate both sides, this will tell us the \cos components: \int _{-L}^L f(x)\cos\left( \frac{m\pi x}{L} \right)\, dx=\frac{a_{0}}{2}\cancelto{ 0 }{ \int _{-L}^L \cos\left( \frac{m\pi x}{L} \right) \, dx }+\sum_{n=1}^\infty\left( a_{n}\int _{-L}^L\cos\left( \frac{n\pi x}{L} \right)\cos\left( \frac{m\pi x}{L} \right) \, dx +b_{n}\int _{-L}^L \sin\left( \frac{n\pi x}{L} \right)\cos\left( \frac{m\pi x}{L} \right)\right) \, dx use trig identities (will be provided on exam): \cos(\alpha)\cos(\beta)=\frac{1}{2}(\cos(\alpha-\beta)+\cos(\alpha+\beta)) \sin(\alpha)\cos(\beta)=\frac{1}{2}(\sin(\alpha+\beta)+\sin(\alpha-\beta)) \sin(\alpha)\sin(\beta)=\frac{1}{2}(\cos(\alpha-\beta)-\cos(\alpha+\beta)) \int _{-L}^L \cos \frac{n\pi x}{L}\cos \frac{m\pi x}{L}\, dx=\frac{1}{2}(\int _{-L}^L \left( \cos(\frac{(n-m)\pi x}{L} )+\cancelto{ 0 }{ \cos(\frac{(n+m)\pi x}{L} })\right)dx = \begin{cases}0 & n\ne m \\L & n=m\end{cases} \int _{-L}^L \sin \frac{n\pi x}{L}\cos \frac{m\pi x}{L} \, dx=\int _{-L}^L \text{odd}\, dx=0 so: \int _{-L} ^L f(x)\cos\left( \frac{m\pi x}{L} \right)\, dx=a_{m}L Similarly can be done for when multiplying both sides by \sin\left( \frac{m\pi x}{L} \right) and integrating both sides to find the \sin coefficients: \int _{-L}^L f(x)\sin\left( \frac{m\pi x}{L} \right)\, dx=\frac{a_{0}}{2}\cancelto{ 0 }{ \int _{-L}^L \sin\left( \frac{m\pi x}{L} \right) \, dx }+\sum_{n=1}^\infty\left( a_{n}\cancelto{ \text{odd} }{ \int _{-L}^L\cos\left( \frac{n\pi x}{L} \right)\sin\left( \frac{m\pi x}{L} \right) } \, dx +b_{n}\int _{-L}^L \sin\left( \frac{n\pi x}{L} \right)\sin\left( \frac{m\pi x}{L} \right)\right) \, dx \int _{-L} ^L \sin\left( \frac{n\pi x}{L} \right)\sin\left( \frac{m\pi x}{L} \right) \, dx=\frac{1}{2}\int_{-L}^L \cos\left(\frac{(n-m)\pi x}{L} \right)-\cos\left( \frac{(n+m)\pi x}{L} \right)dx =\begin{cases}0, & n\ne m \\L, & n=m\end{cases} so: \int _{-L} ^L f(x)\sin\left( \frac{m\pi x}{L} \right)\, dx=b_{m}L In conclusion:

a_{m}=\frac{1}{L}\int _{-L}^L f(x)\cos \frac{m\pi x}{L} \, dx \quad\text{valid for all }m=0,1,2,\dots

b_{m}=\frac{1}{L}\int _{-L}^L f(x)\sin \frac{m\pi x}{L} \, dx=b_{m} \quad m=1,2,\dots

Now we know how to compute the coefficients for Fourier series!

properties: for functions f, g, If \int _{-L}^Lf(x)g(x) \, dx=\begin{cases}0 & f\ne g \\L & f=g \end{cases} then f, g are orthogonal the Fourier expansion is called an ortho normal expansion, Taylor is not orthonormal. #end of lec 28 #start of lec 29 Last lecture we derived how to find the coefficients in a Fourier series. f(x)=\frac{a_{0}}{2}+\sum_{n=1}^\infty\left( a_{n}\cos\left( \frac{n\pi x}{L} \right) + b_{n}\sin\left( \frac{n\pi x}{L}\right) \right) x \in [-L,L]

1st convergence theorem:

If f and f' are piecewise continuous on [-L,L], then the Fourier series converges to: \frac{1}{2}(f(x^-)+f(x^+)) for all x \in (-L,L) and on x=\pm L the Fourier series converges to \frac{1}{2}(f(-L^+)+f(L^-)) 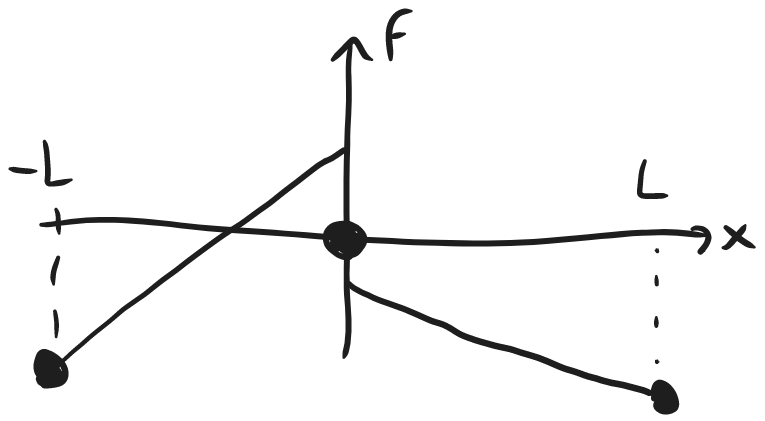Recall the definition of piecewise continuous: f(t) is piecewise continuous on an interval I if f(t) is continuous on I, except possibly at a finite number of points of jump discontinuity (horizontal asymptotes not allowed).

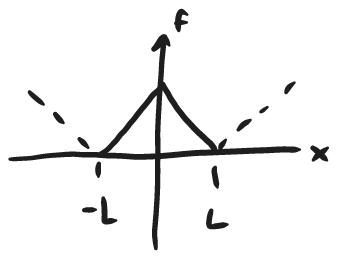
2nd Convergence theorem (uniform convergence):

If f(x) is continuous on (-\infty,\infty) and 2L periodic and if f' is piecewise continuous on [-L,L], then its Fourier series converges to f(x) everywhere (i.e., the Fourier series converges uniformly). #ex #fourier Let's compute the Fourier transform of:

f(x)=\begin{cases}1, & -\pi\leq x\leq 0 \\x, & 0<x\leq \pi\end{cases}

L here is \pi clearly. Let's find the coefficients a_{n} and b_{n} Use the formula we derived earlier: a_{n}=\frac{1}{\pi}\left( \int _{-\pi}^0 1\cos\left( \frac{n\pi x}{\pi} \right)\, dx +\int _{0}^\pi x\cos(nx)\, dx\right) Using integration by parts (for the second integral): =\frac{1}{\pi}\left( \frac{1}{n}\cancelto{ 0 }{ \sin(nx) |_{-\pi}^0} + \frac{1}{n}x\cancelto{ 0 }{ \sin(nx) |_{0}^\pi}-\frac{1}{n}\int _{0}^\pi \sin(nx) \, dx \right) a_{n}=\frac{1}{n^2\pi}(\cos(nx)|_{0}^\pi)=\frac{1}{n^2\pi}(\underbrace{ \cos(n\pi) }_{ (-1)^n }-1) a_{n}=\frac{1}{n^2\pi}((-1)^n-1)\quad n=1,2,\dots Now let's find b_{n} b_{n}=\frac{1}{\pi}\left( \int _{-\pi}^0\sin(nx) \, dx+\int _{0}^\pi x\sin(nx) \, dx \right) =\frac{1}{\pi}[ \frac{-1}{n}\underbrace{ \cos(nx)|_{-\pi}^0 }_{ 1-(-1)^n }-\frac{1}{n}( \underbrace{ x\cos(nx)|_{0}^\pi }_{ \pi(-1)^n-0 }-\underbrace{ \int _{0}^\pi \cos(nx)\, dx }_{ 0 } ) ] b_{n}=\frac{1}{n\pi}((-1)^n-1-\pi(-1)^n) b_{n}=\frac{1}{n\pi}((-1)^n(1-\pi)-1) \quad n=1,2,\dots we find that

a_{2n}=0 \qquad n=1,2,3,\dots

a_{2k-1}=-\frac{2}{n^2\pi} \qquad k=1,2,3\dots

what about when n=0? a_{0}=\frac{1}{\pi}\left( \int _{-\pi}^0 \, dx+\int _{0}^\pi x \, dx \right) a_{0}=\frac{1}{\pi}\left( x|_{-\pi}^0+\frac{x^2}{2}|_{0}^\pi \right) a_{0}=\frac{1}{\pi}\left( 0+\pi+\frac{\pi^2}{2} \right)

a_{0}=\frac{\pi}{2}+1

#ex Let's compute the Fourier transform of:

f(x)=x \qquad -\pi\leq x\leq \pi

We have to take a windowed form of f to make this possible, L=\pi At the left and right edge of the interval, the Fourier series is equal to 0. (1st convergence theorem.) Find the coefficients: a_{n}=\frac{1}{\pi}\int _{-\pi}^\pi x\cos(nx) \, dx=0

a_{n}=0

Why is it zero? because the integrand is an odd function. (odd times even is odd.) and because we are integrating from -\pi to \pi (a symmetric interval) definition of odd: f(x)=-f(-x) definition of even: f(x)=f(-x) odd times even is odd. odd times odd is even. even times even is even. huge exam time saving technique. Find b_{n}: b_{n}=\frac{1}{\pi}\int _{-\pi}^\pi x\sin(nx) \, dx=\frac{2}{\pi}\int _{0}^\pi x\sin(nx) \, dx <- that's even, don't be a silly goose and say it's 0 Using integration by parts: b_{n}=\frac{2}{\pi}\left( x\left( -\frac{1}{n}\cos(nx)|_{0}^\pi \right)-\int_{0}^\pi -\frac{1}{n}\cos(nx) \, dx \right) b_{n}=\frac{2}{\pi}\left( -\frac{\pi}{n}(-1)^n+\frac{1}{n^2}\cancelto{ 0 }{ \sin(nx)|_{0}^\pi } \right)

b_{n}=\frac{2}{n}(-1)^{n+1}

another take away: if f is odd, the \cos terms are 0 if f is even, the \sin terms are 0.

if f is only defined between 0 and L: you can create an odd extension: \bar{f}(x)=\begin{cases}f(x) & 0\leq x\leq L \\-f(-x), & -L\leq x<0 & & \end{cases} this will contain only \sin terms. You also have a choice to extend it as an even function, symmetrically across the y axis. \bar{f}(x)=\begin{cases}f(x) & 0\leq x\leq L \\f(-x), & -L\leq x<0 & & \end{cases} This will contain only \cos terms. #end of lec 29 #start of lec 30 From last lecture: f(x) is defined on [0,L] odd extension: \bar{f}(x)=\begin{cases}f(x), & 0\leq x\leq L \\-f(-x,) & -L\leq x<0\end{cases} and the a coefficients (\cos terms) are zero. not only that, but the b coefficients are: b_{n}=\frac{1}{L}\int _{-L}^L\bar{f}(x) \sin\left( \frac{n\pi x}{L} \right) \, dx

b_{n}=\frac{2}{L}\int _{0}^L f(x)\sin\left( \frac{n\pi x}{L} \right)\, dx

and \bar{f}(x) is:

\bar{f}(x)=\sum_{n=1}^\infty b_{n}\sin\left( \frac{n\pi x}{L} \right)

"How about that, this is called a Fourier sine series." For even extension: \bar{f}(x)=\begin{cases}f(x), & 0\leq x\leq L \\f(-x,) & -L\leq x<0\end{cases} and the b coefficients (\sin terms) are zero. not only that but the a coefficients are: a_{n}=\frac{1}{L}\int _{-L}^L\bar{f}(x) \cos\left( \frac{n\pi x}{L} \right) \, dx

a_{n}=\frac{2}{L}\int _{0}^L f(x)\cos\left( \frac{n\pi x}{L} \right)\, dx

and \bar{f} is:

\bar{f}(x)=\frac{a_{0}}{2}+\sum_{n=1}^\infty a_{n}\cos\left( \frac{n\pi x}{L} \right)

Remember that \sum_{n=1}^\infty b_{n}\sin\left( \frac{n\pi x}{L} \right) was the expansion of the eigen value function from the heat equation? then \frac{a_{0}}{2}+\sum_{n=1}^\infty a_{n}\cos\left( \frac{n\pi x}{L} \right) is also an expansion of some related eigen value function. It's interesting to note.

#ex #fourier Fourier sine series for:

f(x)=x^2 \qquad 0\leq x\leq \pi

Well that means we want the odd extension: 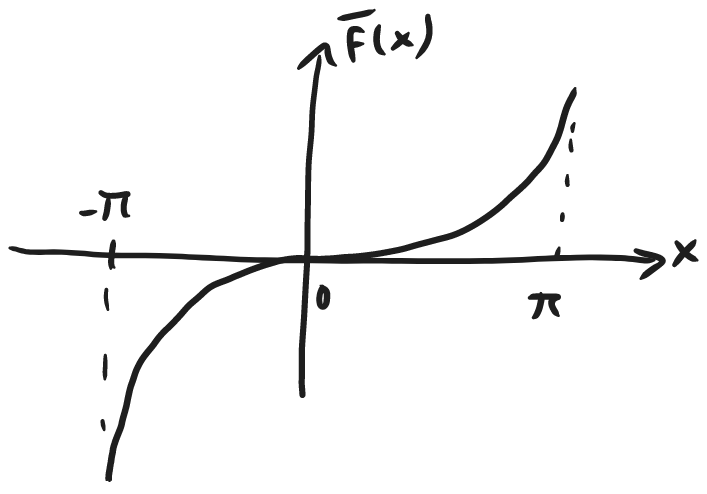the a_{n} (cosine) terms are zero. the b_{n} terms are: b_{n}=\frac{2}{\pi}\int _{0}^\pi x^2\sin(nx) \, dx =-\frac{2}{n\pi}\left[ x^2\cos(nx)|_{0}^\pi-2\int _{0}^\pi x\cos(nx)\, dx \right] =-\frac{2}{n\pi}\left[ \pi^2(-1)^n-\frac{2}{n}\left( x\cancelto{ 0 }{ \sin(nx) }|_{0}^\pi-\int _{0}^\pi \sin(nx)\, dx \right) \right] b_{n}=-\frac{2}{n\pi}[ \pi^2(-1)^n-\frac{2}{n^2}\underbrace{ \cos(nx)|_{0}^\pi }_{ (-1)^n-1 }]=\frac{2\pi}{n}(-1)^{n+1}+\frac{4}{n^3\pi}((-1)^n-1) for n=1,2,3,\dots Note no n=0 so no division by zero problems here.

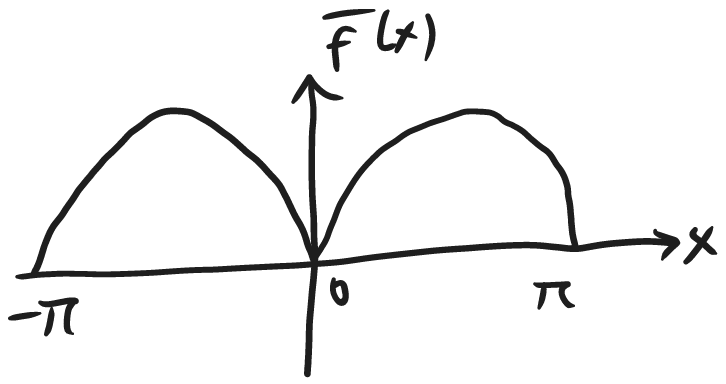
#ex #fourier Fourier cosine series of f(x)=\sin(x) for 0\leq x\leq \pi b_{n} (sine) terms are all zero obviously, as it's asking for a Fourier cosine series, i.e., we are doing an even extension. a_{n}=\frac{2}{\pi}\int _{0}^\pi \sin(x)\cos(nx)\, dx for n=0,1,2,\dots <-Odd, but not symmetrical bounds. We can't rule out that it's zero.

Don't be a silly goose and try changing the bounds by removing that 2 in the front. If you did, you'd also have to change \sin(x) to \bar{f} which is abs(\sin(x)) and then you're integrating a_{n}=\frac{1}{\pi}\int _{-\pi}^\pi |\sin(x)|\cos(nx)\, dx which is even$\times$even.

Use trig identity: (by the way the identities will be provided in the final exam.) =\frac{2}{\pi} \frac{1}{2}\int _{0}^\pi \left[\sin((1-n)x)+\sin((n+1)x)\right]\, dx Integrating gives you: \frac{1}{\pi}( \frac{-1}{1-n}\underbrace{ \cos((1-n)x)|_{0}^\pi }_{ (-1)^{n+1}-1 } +\frac{-1}{n+1}\underbrace{ \cos((n+1)x)|_{0}^\pi }_{ (-1)^{n+1}-1 }) a_{n}=-\frac{1}{\pi} \frac{1}{n+1}(-1)^{n+1}+\frac{1}{\pi} \frac{1}{n+1}+\frac{1}{\pi} \frac{1}{-(1-n)}(-1)^{n+1}+\frac{1}{\pi} \frac{1}{1-n} a_{n}=-\frac{1}{\pi} \frac{1}{n+1} (-1)^{n+1}+\frac{1}{\pi} \frac{1}{n+1}+\frac{1}{\pi} \frac{1}{n-1}(-1)^{n-1}-\frac{1}{\pi} \frac{1}{n-1} Assuming that n\ne0,1. (note: n=-1 is a non-issue since negative coefficients are never considered when taking a Fourier transform.) So what is a_{0}, a_{1}? a_{0}=\frac{2}{\pi}\int _{0}^\pi \sin(x) \, dx=\frac{4}{\pi} a_{1}=\frac{2}{\pi}\int _{0}^\pi \sin(x)\cos(x) \, dx=\frac{1}{\pi}\int _{0}^\pi \sin(2x)\, dx=0 "zero is a very very special number it took humanity many numbers of years to invent zero" referring to when dividing by 0. Additionally we know that the terms cancel when: a_{2k-1}=0 for k=1,2,\dots a_{2k}=\frac{2}{\pi} \frac{1}{2k+1}-\frac{2}{\pi} \frac{1}{2k-1} for k=1,2,\dots then:

\bar{f}(x)=\frac{2}{\pi}+\frac{2}{\pi}\sum_{k=1}^\infty\left( \frac{1}{2k+1}-\frac{1}{2k-1} \right)\cos(2k\pi x)

Even with 10 terms, we get a pretty good approximation: 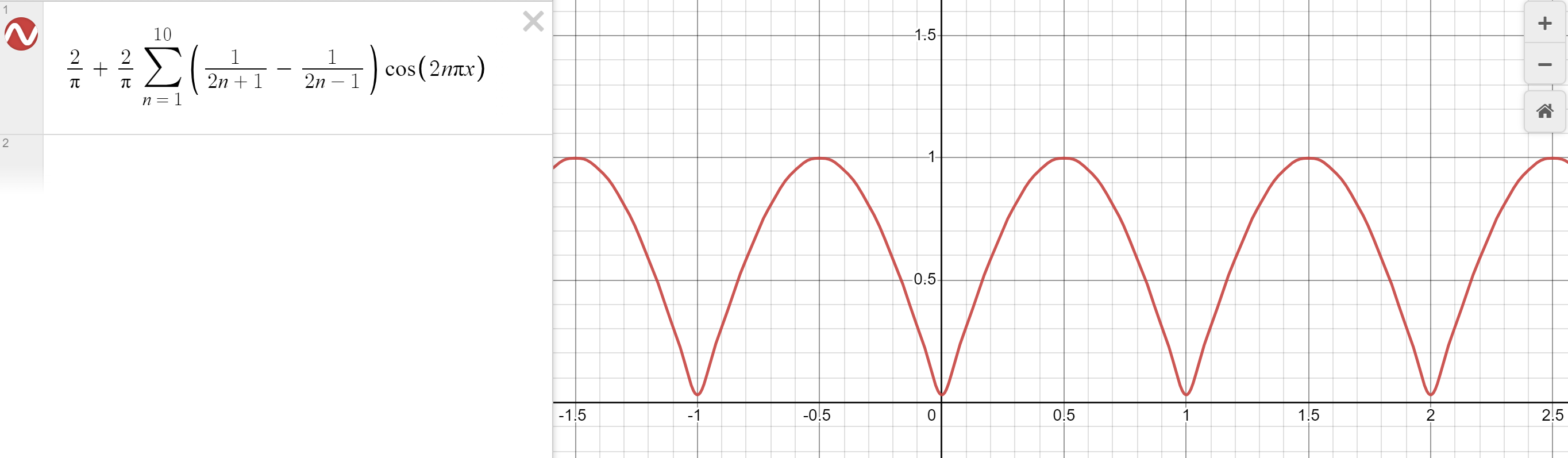We have prepared ourselves now, now we start solving PDE's. He's encouraging us to attend the lectures in these last two weeks. He's making it sound like PDE's are hard.