#fourier
Remember the heat flow equation? We obtained that it's solution could be expressed in the form: 
$$\sum_{n=1}^\infty c_{n}\sin\left( \frac{n\pi x}{L} \right)\quad\text{for}\quad0\leq x\leq L$$
But what is $c_{n}$? They are the coefficients of a Fourier transform. We want to develop a way to compute them.
Let's derive how to compute the coefficients of a Fourier transform. (feel free to skip to the end)
$f(x)=\sum_{n=1}^\infty b_{n}\sin\left( \frac{n\pi x}{L} \right)$ where $L$ is length of the rod

This is a Fourier series: it's a more general form of what we have above.
$f(x)=\frac{a_{0}}{2}+\sum_{n=1}^\infty\left( a_{n}\cos\left( \frac{n\pi x}{L} \right) + b_{n}\sin\left( \frac{n\pi x}{L}\right) \right)$
$x \in [-L,L]$
It converges to $f(x)$ almost everywhere (convergence will be discussed below)
Has a lot of benefits over Taylor series. $f(x)$ doesn't have to be infinitely differentiable (analytic)
$f(x)$ can even have jump discontinuities
Let's assume the equation is true when $x \in [-L,L]$
Integrate both sides, it will tell us the DC offset:
$\int _{-L} ^L f(x) \, dx=\int _{-L}^L \frac{a_{0}}{2} \, dx+\int _{-L}^L (\text{put summation here}) \, dx$
$\int _{-L}^L \cos\left( \frac{n\pi x}{L} \right) \, dx=\frac{L}{n\pi}\sin\left( \frac{n\pi x}{L} \right)|_{-L}^L=0$
same for $\int _{-L}^L \sin\left( \frac{n\pi x}{L} \right)\, dx=0$ (it equals 0)
so
$\int _{-L} ^L f(x) \, dx=\int _{-L}^L \frac{a_{0}}{2} \, dx+\int _{-L}^L0 \, dx$
$\int _{-L} ^L f(x) \, dx=a_{0}L$
$a_{0}=\frac{1}{L}\int _{-L}^{L} f(x) \, dx$
Now let's multiply both sides by $\cos\left( \frac{m\pi x}{L} \right)$ and integrate both sides, this will tell us the $\cos$ components:
$\int _{-L}^L f(x)\cos\left( \frac{m\pi x}{L} \right)\, dx=\frac{a_{0}}{2}\cancelto{ 0 }{ \int _{-L}^L \cos\left( \frac{m\pi x}{L} \right) \, dx }+\sum_{n=1}^\infty\left( a_{n}\int _{-L}^L\cos\left( \frac{n\pi x}{L} \right)\cos\left( \frac{m\pi x}{L} \right) \, dx +b_{n}\int _{-L}^L \sin\left( \frac{n\pi x}{L} \right)\cos\left( \frac{m\pi x}{L} \right)\right) \, dx$
use trig identities (will be provided on exam):
$\cos(\alpha)\cos(\beta)=\frac{1}{2}(\cos(\alpha-\beta)+\cos(\alpha+\beta))$
$\sin(\alpha)\cos(\beta)=\frac{1}{2}(\sin(\alpha+\beta)+\sin(\alpha-\beta))$
$\sin(\alpha)\sin(\beta)=\frac{1}{2}(\cos(\alpha-\beta)-\cos(\alpha+\beta))$
$\int _{-L}^L \cos \frac{n\pi x}{L}\cos \frac{m\pi x}{L}\, dx=\frac{1}{2}(\int _{-L}^L \left( \cos(\frac{(n-m)\pi x}{L} )+\cancelto{ 0 }{ \cos(\frac{(n+m)\pi x}{L} })\right)dx$
$= \begin{cases}0 & n\ne m \\L & n=m\end{cases}$
$\int _{-L}^L \sin \frac{n\pi x}{L}\cos \frac{m\pi x}{L} \, dx=\int _{-L}^L \text{odd}\, dx=0$
so:
$\int _{-L} ^L f(x)\cos\left( \frac{m\pi x}{L} \right)\, dx=a_{m}L$
Similarly can be done for when multiplying both sides by $\sin\left( \frac{m\pi x}{L} \right)$ and integrating both sides to find the $\sin$ coefficients:
$\int _{-L}^L f(x)\sin\left( \frac{m\pi x}{L} \right)\, dx=\frac{a_{0}}{2}\cancelto{ 0 }{ \int _{-L}^L \sin\left( \frac{m\pi x}{L} \right) \, dx }+\sum_{n=1}^\infty\left( a_{n}\cancelto{ \text{odd} }{ \int _{-L}^L\cos\left( \frac{n\pi x}{L} \right)\sin\left( \frac{m\pi x}{L} \right) } \, dx +b_{n}\int _{-L}^L \sin\left( \frac{n\pi x}{L} \right)\sin\left( \frac{m\pi x}{L} \right)\right) \, dx$
$\int _{-L} ^L \sin\left( \frac{n\pi x}{L} \right)\sin\left( \frac{m\pi x}{L} \right) \, dx=\frac{1}{2}\int_{-L}^L \cos\left(\frac{(n-m)\pi x}{L} \right)-\cos\left( \frac{(n+m)\pi x}{L} \right)dx$
$=\begin{cases}0, & n\ne m \\L, & n=m\end{cases}$
so:
$\int _{-L} ^L f(x)\sin\left( \frac{m\pi x}{L} \right)\, dx=b_{m}L$
In conclusion:
$$a_{m}=\frac{1}{L}\int _{-L}^L f(x)\cos \frac{m\pi x}{L} \, dx \quad\text{valid for all }m=0,1,2,\dots$$
$$b_{m}=\frac{1}{L}\int _{-L}^L f(x)\sin \frac{m\pi x}{L} \, dx=b_{m} \quad m=1,2,\dots$$
Now we know how to compute the coefficients for Fourier series!

properties:
for functions $f$, $g$, If $\int _{-L}^Lf(x)g(x) \, dx=\begin{cases}0 & f\ne g \\L & f=g \end{cases}$
then $f, g$ are orthogonal
the Fourier expansion is called an ortho normal expansion, Taylor is not orthonormal.
#end of lec 28
#start of lec 29
Last lecture we derived how to find the coefficients of a Fourier series.
$f(x)=\frac{a_{0}}{2}+\sum_{n=1}^\infty\left( a_{n}\cos\left( \frac{n\pi x}{L} \right) + b_{n}\sin\left( \frac{n\pi x}{L}\right) \right)$
$x \in [-L,L]$
### 1st convergence theorem:
If $f$ and $f'$ are piecewise continuous on $[-L,L]$, then the Fourier series converges to:
$\frac{1}{2}(f(x^-)+f(x^+))$ for all $x \in (-L,L)$
and on $x=\pm L$ the Fourier series converges to $\frac{1}{2}(f(-L^+)+f(L^-))$
![draw](drawings/Drawing-2023-11-22-13.15.26.excalidraw.png)
Recall the definition of piecewise continuous: $f(t)$ is piecewise continuous on an interval $I$ if $f(t)$ is continuous on $I$, except possibly at a <u>finite</u> number of points of <u>jump</u> discontinuity (horizontal asymptotes not allowed).
### 2nd Convergence theorem (uniform convergence):
If $f(x)$ is continuous on $(-\infty,\infty)$ and $2L$ periodic and if $f'$ is piecewise continuous on $[-L,L]$, then its Fourier series converges to $f(x)$ everywhere (i.e., the Fourier series converges uniformly).
![draw](drawings/Drawing-2023-11-22-13.14.05.excalidraw.png)
#ex #fourier 
Let's compute the Fourier transform of:
$$f(x)=\begin{cases}1, & -\pi\leq x\leq 0 \\x, & 0<x\leq \pi\end{cases}$$
$L$ here is $\pi$ clearly.
Let's find the coefficients $a_{n}$ and $b_{n}$
Use the formula we derived earlier:
$a_{n}=\frac{1}{\pi}\left( \int _{-\pi}^0 1\cos\left( \frac{n\pi x}{\pi} \right)\, dx +\int _{0}^\pi x\cos(nx)\, dx\right)$
Using integration by parts (for the second integral):
$=\frac{1}{\pi}\left( \frac{1}{n}\cancelto{ 0 }{ \sin(nx) |_{-\pi}^0} + \frac{1}{n}x\cancelto{ 0 }{ \sin(nx) |_{0}^\pi}-\frac{1}{n}\int _{0}^\pi \sin(nx) \, dx \right)$
$a_{n}=\frac{1}{n^2\pi}(\cos(nx)|_{0}^\pi)=\frac{1}{n^2\pi}(\underbrace{ \cos(n\pi) }_{ (-1)^n }-1)$
$a_{n}=\frac{1}{n^2\pi}((-1)^n-1)\quad n=1,2,\dots$
Now let's find $b_{n}$
$b_{n}=\frac{1}{\pi}\left( \int _{-\pi}^0\sin(nx) \, dx+\int _{0}^\pi x\sin(nx) \, dx \right)$
$=\frac{1}{\pi}[  \frac{-1}{n}\underbrace{ \cos(nx)|_{-\pi}^0 }_{ 1-(-1)^n }-\frac{1}{n}(  \underbrace{ x\cos(nx)|_{0}^\pi }_{ \pi(-1)^n-0 }-\underbrace{ \int _{0}^\pi \cos(nx)\, dx  }_{ 0 } ) ]$
$b_{n}=\frac{1}{n\pi}((-1)^n-1-\pi(-1)^n)$
$b_{n}=\frac{1}{n\pi}((-1)^n(1-\pi)-1) \quad n=1,2,\dots$
we find that
$$a_{2n}=0 \qquad n=1,2,3,\dots$$
$$a_{2k-1}=-\frac{2}{n^2\pi} \qquad k=1,2,3\dots$$
what about when $n=0$?
$a_{0}=\frac{1}{\pi}\left( \int _{-\pi}^0 \, dx+\int _{0}^\pi x \, dx \right)$
$a_{0}=\frac{1}{\pi}\left( x|_{-\pi}^0+\frac{x^2}{2}|_{0}^\pi \right)$
$a_{0}=\frac{1}{\pi}\left( 0+\pi+\frac{\pi^2}{2} \right)$
$$a_{0}=\frac{\pi}{2}+1$$

#ex Let's compute the Fourier transform of:
$$f(x)=x \qquad -\pi\leq x\leq \pi$$
We have to take a windowed form of $f$ to make this possible, $L=\pi$
At the left and right edge of the interval, the Fourier series is equal to 0. (1st convergence theorem.)
Find the coefficients:
$a_{n}=\frac{1}{\pi}\int _{-\pi}^\pi x\cos(nx) \, dx=0$
$$a_{n}=0$$
Why is it zero? because the integrand is an odd function. (odd times even is odd.) and because we are integrating from $-\pi$ to $\pi$ (a symmetric interval)
definition of odd: $f(x)=-f(-x)$
definition of even: $f(x)=f(-x)$
odd times even is odd.
odd times odd is even.
even times even is even.
huge exam time saving technique.
Find $b_{n}$:
$b_{n}=\frac{1}{\pi}\int _{-\pi}^\pi x\sin(nx) \, dx=\frac{2}{\pi}\int _{0}^\pi x\sin(nx) \, dx$ <- that's even, don't be a silly goose and say it's $0$
Using integration by parts:
$b_{n}=\frac{2}{\pi}\left( x\left( -\frac{1}{n}\cos(nx)|_{0}^\pi \right)-\int_{0}^\pi -\frac{1}{n}\cos(nx) \, dx \right)$
$b_{n}=\frac{2}{\pi}\left( -\frac{\pi}{n}(-1)^n+\frac{1}{n^2}\cancelto{ 0 }{ \sin(nx)|_{0}^\pi } \right)$
$$b_{n}=\frac{2}{n}(-1)^{n+1}$$
another take away: if $f$ is odd, the $\cos$ terms are $0$
if $f$ is even, the $\sin$ terms are $0$.

if $f$ is only defined between $0$ and $L$:
you can create an odd extension: $\bar{f}(x)=\begin{cases}f(x)  & 0\leq x\leq L \\-f(-x), & -L\leq x<0 &  & \end{cases}$
this will contain only $\sin$ terms.
You also have a choice to extend it as an even function, symmetrically across the $y$ axis.
$\bar{f}(x)=\begin{cases}f(x)  & 0\leq x\leq L \\f(-x), & -L\leq x<0 &  & \end{cases}$
This will contain only $\cos$ terms.
#end of lec 29 
#start of lec 30
From last lecture: 
$f(x)$ is defined on $[0,L]$
odd extension:
$\bar{f}(x)=\begin{cases}f(x), & 0\leq x\leq L \\-f(-x,) & -L\leq x<0\end{cases}$
and the $a$ coefficients ($\cos$ terms) are zero.
not only that, but the $b$ coefficients are:
$b_{n}=\frac{1}{L}\int _{-L}^L\bar{f}(x) \sin\left( \frac{n\pi x}{L} \right) \, dx$
$$b_{n}=\frac{2}{L}\int _{0}^L f(x)\sin\left( \frac{n\pi x}{L} \right)\, dx$$
and $\bar{f}(x)$ is:
$$\bar{f}(x)=\sum_{n=1}^\infty b_{n}\sin\left( \frac{n\pi x}{L} \right)$$
"How about that, this is called a Fourier sine series."
For even extension:
$\bar{f}(x)=\begin{cases}f(x), & 0\leq x\leq L \\f(-x,) & -L\leq x<0\end{cases}$
and the $b$ coefficients ($\sin$ terms) are zero.
not only that but the $a$ coefficients are:
$a_{n}=\frac{1}{L}\int _{-L}^L\bar{f}(x) \cos\left( \frac{n\pi x}{L} \right) \, dx$
$$a_{n}=\frac{2}{L}\int _{0}^L f(x)\cos\left( \frac{n\pi x}{L} \right)\, dx$$
and $\bar{f}$ is:
$$\bar{f}(x)=\frac{a_{0}}{2}+\sum_{n=1}^\infty a_{n}\cos\left( \frac{n\pi x}{L} \right)$$
Remember that $\sum_{n=1}^\infty b_{n}\sin\left( \frac{n\pi x}{L} \right)$ was the expansion of the eigen value function from the heat equation?
then $\frac{a_{0}}{2}+\sum_{n=1}^\infty a_{n}\cos\left( \frac{n\pi x}{L} \right)$ is also an expansion of some related eigen value function. It's interesting to note.

#ex #fourier Fourier sine series for: 
$$f(x)=x^2 \qquad 0\leq x\leq \pi$$
Well that means we want the odd extension:
![draw](drawings/Drawing-2023-11-24-13.15.17.excalidraw.png)
the $a_{n}$ (cosine) terms are zero.
the $b_{n}$ terms are:
$b_{n}=\frac{2}{\pi}\int _{0}^\pi x^2\sin(nx) \, dx$
$=-\frac{2}{n\pi}\left[ x^2\cos(nx)|_{0}^\pi-2\int _{0}^\pi x\cos(nx)\, dx \right]$
$=-\frac{2}{n\pi}\left[ \pi^2(-1)^n-\frac{2}{n}\left( x\cancelto{ 0 }{ \sin(nx) }|_{0}^\pi-\int _{0}^\pi \sin(nx)\, dx \right) \right]$
$b_{n}=-\frac{2}{n\pi}[ \pi^2(-1)^n-\frac{2}{n^2}\underbrace{ \cos(nx)|_{0}^\pi }_{ (-1)^n-1 }]=\frac{2\pi}{n}(-1)^{n+1}+\frac{4}{n^3\pi}((-1)^n-1)$ for $n=1,2,3,\dots$
Note no $n=0$ so no division by zero problems here.

#ex #fourier Fourier cosine series of $f(x)=\sin(x)$ for $0\leq x\leq \pi$
![draw](drawings/Drawing-2023-11-24-13.23.08.excalidraw.png)
$b_{n}$ (sine) terms are all zero obviously, as it's asking for a Fourier cosine series, i.e., we are doing an even extension.
$a_{n}=\frac{2}{\pi}\int _{0}^\pi \sin(x)\cos(nx)\, dx$ for $n=0,1,2,\dots$ <-Odd, but not symmetrical bounds. We can't rule out that it's zero.
>Don't be a silly goose and try changing the bounds by removing that 2 in the front. If you did, you'd also have to change $\sin(x)$ to $\bar{f}$ which is $abs(\sin(x))$ and then you're integrating $a_{n}=\frac{1}{\pi}\int _{-\pi}^\pi |\sin(x)|\cos(nx)\, dx$ which is even$\times$even.

Use trig identity: (by the way the identities will be provided in the final exam.)
$=\frac{2}{\pi} \frac{1}{2}\int _{0}^\pi \left[\sin((1-n)x)+\sin((n+1)x)\right]\, dx$
Integrating gives you:
$\frac{1}{\pi}( \frac{-1}{1-n}\underbrace{ \cos((1-n)x)|_{0}^\pi }_{ (-1)^{n+1}-1 } +\frac{-1}{n+1}\underbrace{ \cos((n+1)x)|_{0}^\pi }_{ (-1)^{n+1}-1 })$
$a_{n}=-\frac{1}{\pi} \frac{1}{n+1}(-1)^{n+1}+\frac{1}{\pi} \frac{1}{n+1}+\frac{1}{\pi} \frac{1}{-(1-n)}(-1)^{n+1}+\frac{1}{\pi} \frac{1}{1-n}$
$a_{n}=-\frac{1}{\pi} \frac{1}{n+1} (-1)^{n+1}+\frac{1}{\pi} \frac{1}{n+1}+\frac{1}{\pi} \frac{1}{n-1}(-1)^{n-1}-\frac{1}{\pi} \frac{1}{n-1}$
Assuming that $n\ne0,1$. (note: $n=-1$ is a non-issue since negative coefficients are never considered when taking a Fourier transform.)
So what is $a_{0}, a_{1}$?
$a_{0}=\frac{2}{\pi}\int _{0}^\pi \sin(x) \, dx=\frac{4}{\pi}$
$a_{1}=\frac{2}{\pi}\int _{0}^\pi \sin(x)\cos(x) \, dx=\frac{1}{\pi}\int _{0}^\pi \sin(2x)\, dx=0$
<i>"zero is a very very special number it took humanity many numbers of years to invent zero"</i> referring to when dividing by 0.
Additionally we know that the terms cancel when:
$a_{2k-1}=0$ for $k=1,2,\dots$
$a_{2k}=\frac{2}{\pi} \frac{1}{2k+1}-\frac{2}{\pi} \frac{1}{2k-1}$ for $k=1,2,\dots$
then:
$$\bar{f}(x)=\frac{2}{\pi}+\frac{2}{\pi}\sum_{k=1}^\infty\left( \frac{1}{2k+1}-\frac{1}{2k-1} \right)\cos(2k\pi x)$$
Even with 10 terms, we get a pretty good approximation:
![fouriercosineofsin.png](drawings/fouriercosineofsin.png)
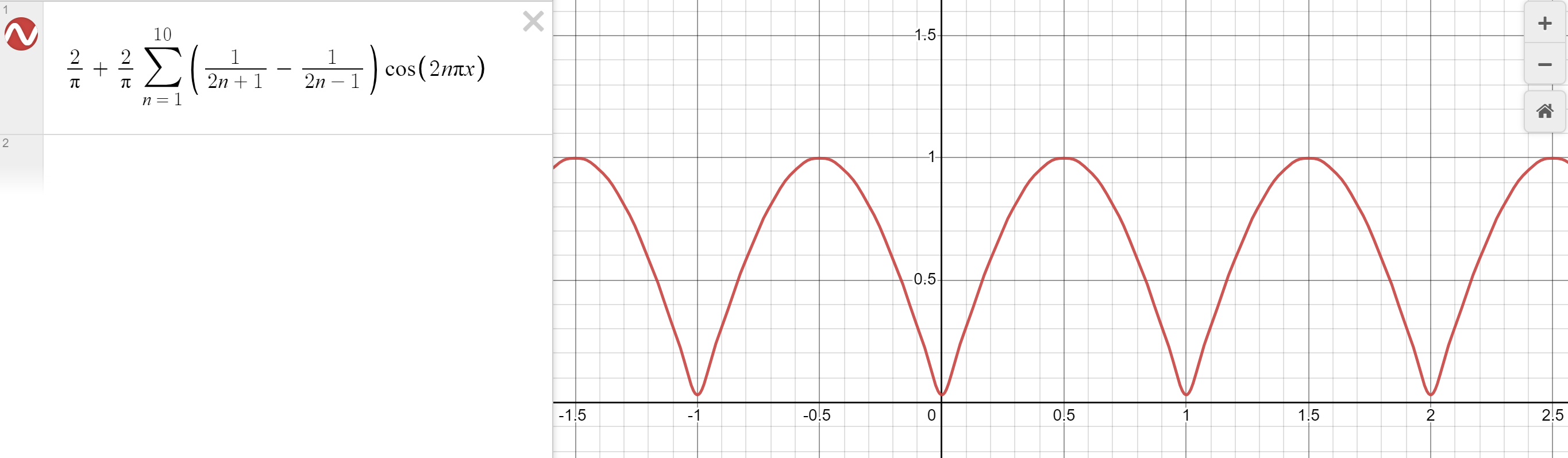
Here's a little script I wrote to generate an audible waveform of this Fourier series!
<html>

<head>

<script src="https://code.jquery.com/jquery-2.1.1.min.js"></script>
  <meta charset="utf-8">
</head>

<body>

  <button id="playButton">Play the sound</button>

  <canvas id='scope'></canvas>

  <canvas id='spectrum'></canvas>

<div class="slidecontainer">
<p>Number of harmonics: <span id="textHarmonics"></span></p>
  <input type="range" min="0" max="100" value="50" style="width: 500px;" id="sliderHarmonics">

</div>

<div class="slidecontainer">
  <p>Frequency: <span id="textFreq"></span></p>
  <input type="range" min="0" max="440" value="220" style="width: 500px;" id="sliderFreq">



</div>

<script src="playaudio.js"></script>

</body>

</html>

We have prepared ourselves now, now we start solving PDE's. He's encouraging us to attend the lectures in these last two weeks. He's making it sound like PDE's are hard.