Let's consider a guitar string:
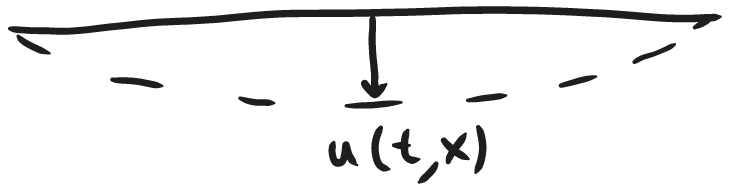
assuming the thickness of the string is much smaller than the length of the string, which is true.
$\frac{ \partial u^2 }{ \partial t^2 }=\alpha^2 \frac{ \partial^2 u }{ \partial x^2 }\qquad 0\leq x\leq L,\quad t>0$
^ Reminds me of the wave equation from Phys 130.
Since the string is tied down on the ends we have the following initial conditions:
$u(t,0)=u(t,L)=0 \qquad t>0$
$u(0,x)=f(x) \qquad 0\leq x\leq L$ <- position of each segment of string at $t=0$
$\frac{ \partial u }{ \partial t }(0,x)=g(x) \qquad 0\leq x\leq L$ <- velocity of each segment of string at at $t=0$
^IBVP of the system.
#end of lec 33
#start of lec 34
The wave equation follows many phenomena in electrical engineering.
separation of variables:
$u(t,x)=X(x)T(t)$
plug in to equation:
$T''X=\alpha^2TX''$
$\frac{T''}{\alpha^2T}=\frac{X''}{X}=-\lambda$ <- eigen value problem #evp
consider the $X$ side:
$X''+\lambda X=0, \quad X(0)=X(L)=0$
We've solved this before (in lec 27).
The only non-trivial solutions are:
$\lambda_{n}=(\frac{n\pi}{L})^2$
$X_{n}(x)=\sin\left( \frac{n\pi x}{L} \right)$ for $n=1,2,3,\dots$
$\frac{T''}{\alpha^2T}=-\left( \frac{n\pi}{L} \right)^2$
$T_{n}''+\left( \frac{\alpha n\pi}{L} \right)^2T_{n}=0$
Unlike before where we could integrate both sides, we can't here! Last time it was a separable equation, now this one is a second order linear equation, and we must solve it as such.
characteristic equation:
$r^2+\left( \frac{\alpha n\pi}{L} \right)^2=0$
$r_{1,2}=\pm i \frac{\alpha n\pi}{L}$
"Don't memorize the steps. If you try to memorize you will mess up the final for sure. Ask yourself, why am I doing this here?"
$T_{n}(t)=b_{n}\cos\left( \frac{\alpha n\pi}{L}t \right)+a_{n}\sin\left( \frac{\alpha n\pi}{L}t \right)$
$u_{n}(t,x)=\left( b_{n}\cos\left( \frac{\alpha n\pi}{L}t \right)+a_{n}\sin\left( \frac{\alpha n\pi}{L}t \right) \right)\sin\left( \frac{n\pi x}{L} \right)$
if you sum all these modes, you get the solution:
$$u_{n}(t,x)=\sum_{n=1}^\infty\left( b_{n}\cos\left( \frac{\alpha n\pi}{L} t\right)+a_{n}\sin\left( \frac{\alpha n\pi}{L}t \right) \right)\sin\left( \frac{n\pi x}{L} \right)$$
"mathematics and reality do align very well, if the speed of the string is different [by varying $\alpha$] the solution differs as well."
The first initial condition gives:
$u(0,x)=f(x)=\sum_{n=1}^\infty b_{n}\sin\left( \frac{n\pi x}{L} \right)$
$$\implies b_{n}=\frac{2}{L}\int _{0}^L f(x)\sin\left( \frac{n\pi x}{L} \right) \, dx$$
Where does it converge? Well in real life your string, $f(x)$, is continuous and your $f'(x)$ is piecewise continuous, so it will converge everywhere. If $f(x)$ was discontinuous in real life that would mean your string has a break in it.
The second initial condition gives:
$\frac{ \partial u }{ \partial t }(0,x)=g(x)=\sum_{n=1}^\infty a_{n} \frac{\alpha n\pi}{L}\sin\left( \frac{\alpha n\pi}{L} \right)$
$a_{n} \frac{\alpha n\pi}{L}$ are the Fourier $\sin$ coefficients of $g(x)$
$\implies a_{n} \frac{\alpha n\pi}{L}=\frac{2}{L}\int _{0}^L g(x)\sin\left( \frac{n\pi x}{L} \right)\, dx$
$$a_{n}=\frac{2}{\alpha n\pi}\int _{0}^L g(x)\sin\left( \frac{n\pi x}{L} \right)\, dx$$
$\alpha^2$ is the Hooke modulus of the string btw.
^ This is a good general formula for computing wave equations, as long as the initial conditions match up, you can just plug in your values and you're done.
Remember the heat equation, the amplitude is exponentially decreasing,
here the amplitude is oscillatory and doesn't decrease in time. boi-oi-oi-oing.
To make it more realistic we have to add a term for resistance, and we end up with a $b$ in the characteristic equation for T.
btw this equation models the electromagnetic field, to some approximation.
the lowest mode is called the fundamental mode, the following terms after are called harmonics.
If two instruments play the same note (same fundamental frequency), they sound different! and that's because of their difference in harmonics.
The modes are standing waves in the string.
"My claim, and this is not just my claim [...], is that any object, including social objects, can be described by waves. [...] Everything is a wave."
You can model elementary particle behaviours with solitons (non linear waves.)
In life in the real world, all waves have finite speed.
So that's why its important to learn the wave equation. It's the prototype to waves.
"Waves are the fundamental object. [...]. So that's why it's important, these are the fundamental objects of nature here."
So, let's try an example using our formula above:
$f(x)=\begin{cases}x, & 0\leq x\leq \frac{\pi}{2}\\ \ \pi-x, & \frac{\pi}{2}
Plug in:
$b_{n}=\frac{2}{\pi}\left( \int _{0} ^\frac{\pi}{2} x\sin(nx) \, dx +\int _{\frac{\pi}{2}} ^\pi (\pi-x)\sin(nx) \, dx\right)$
Skip some integration:
$b_{n}=\frac{4}{n^2\pi}\sin\left( \frac{n\pi}{2} \right)$
half of the b coefficients are 0.
$b_{2k}=0$ for $k=1,2,\dots$
$b_{2k-1}=\frac{4}{(2k-1)^2\pi}(-1)^{k+1}$ for $k=1,2,\dots$
Plug in g(x) to get $a_n$ terms
however, there's a short cut here. From definition of $g(x)$ earlier:
$g(x)=\sum_{n=1}^\infty a_{n} \frac{\alpha n\pi}{L}\sin\left( \frac{\alpha n\pi}{L} \right)$
$g(x)=a_{1}\sin(x)+2a_{2}\sin(2x)+3a_{3}\sin(3x)+\dots$
but $g(x)$ is $\sin(x)$.
so $a_{1}=1$ and every other term is 0
plug this in to get the solution:
$$u(t,x)=\sin (t)\sin(x)+\sum_{k=1}^\infty \frac{4(-1)^{k+1}}{\pi(2k-1)^2}\cos((2k-1)t)\sin((2k-1)x)$$
Peep this gif:
red is $f(x)$, purple is $u(t,x)$. Looks kinda stringy in behavior!
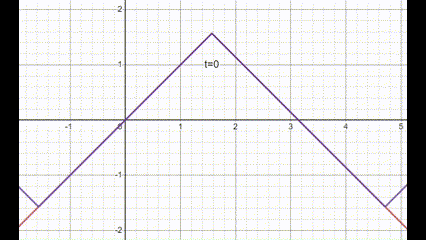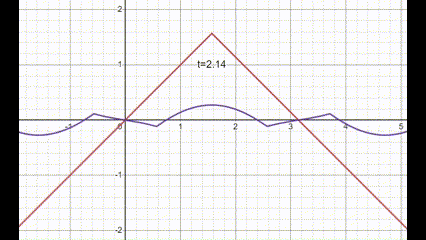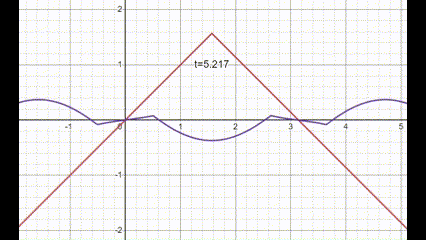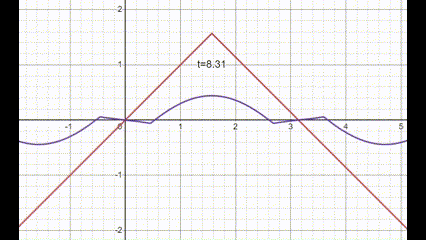
I was kinda confused from the plot, if the initial speed is $g(x)=\sin(x)$ then shouldn't that string peak pop up a bit before heading down? Because it has an initial speed of $g\left( \frac{\pi}{2} \right)=1$ in the upwards direction. Surprisingly the answer is no, the string experiences infinite acceleration in the downwards direction at that pinch point at $t=0$. So the initial speed at $x=\frac{\pi}{2}$ goes to zero as soon as the string is put into motion. How strange is that! Imagine being an ant on the string, as soon as any "pinch point" on the string reaches you, you would be knocked right off, either the floor suddenly drops from beneath your feet or the floor pushes up and crushes you.
#end of lec 34
#start of lec 35
Last problem of the course which we will finish today.
$$\frac{ \partial^2 u }{ \partial t^2 }=\frac{ \partial^2 u }{ \partial x^2 }+tx \qquad 0\leq x\leq \pi, \quad t>0$$
That's a driven wave equation. $tx$ is the source term.
$$u(0,t)=u(\pi,t)=0 \qquad t>0$$
$$u(x,0)=\sin(x) \qquad 0\leq x\leq \pi$$
$$\frac{ \partial u }{ \partial t }(x,0)=5\sin(2x)-3\sin(5x)\qquad 0\leq x\leq \pi$$
when $tx$ wasn't there in last problem we had the solution:
$u(t,x)=\sum_{n=1}^\infty \underbrace{ (a_{n}\cos(nt)+b_{n}\sin(nt)) }_{ u_{n}(t) }\sin(nx)$ notice $L=\pi$
since $u(0,t)=u(\pi,t)=0$ we can expect a solution of the form:
$u(x,t)=\sum_{n=1}^\infty u_{n}(t)\sin\left( \frac{n\pi x}{\pi} \right)$
If any of the boundary conditions are non zero, then we have to split(?) into X and T. (needs verification)
If we expand $tx$ as a Fourier series:
$tx=\sum_{n=1}^\infty h_{n}\sin(nx)$ (this is called a formal expansion, the two actually aren't exactly equal due to the discontinuity in $tx$.)
$h_{n}=\frac{2}{\pi}\int _{0} ^\pi tx\sin(nx)\, dx$
here's a plot of the formal expansion of $tx$. The solid line represents $tx$ and the dotted line represents what $tx$ will look like in the future as $t$ increases. This value $tx$ is proportional to a pulling force placed on each point on the string. So we should expect the string to be stretched out! As you'll see in the last plot.
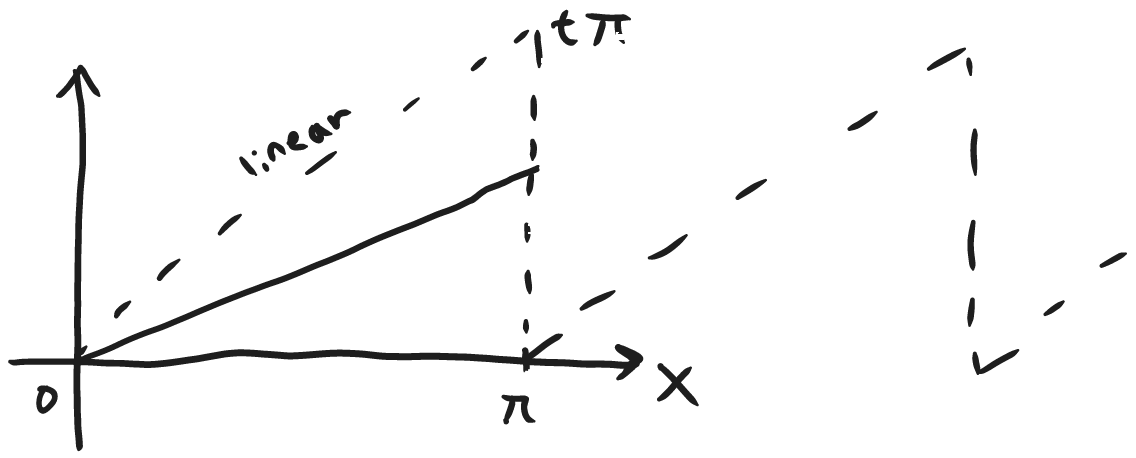
Continuous between $0$ and $\pi$ but on the edge points, the Fourier sine series will converge to the midpoint of the two edge points.
Integrate by parts:
$h_{n}=\frac{2t}{\pi}\int _{0}^\pi x\sin(nx)\, dx=- \frac{2t}{\pi n}\left( x\cos(nx)|_{0}^\pi-\int _{0}^\pi \cancel{ \cos(nx) }\, dx \right)$
$h_{n}(t)=\frac{2t}{n}(-1)^{n+1}$
$h(x,t)=tx=\sum_{n=1}^\infty h_{n}\sin(nx)=\sum_{n=1}^\infty \frac{2t}{n}(-1)^{n+1}\sin(nx)$
$\frac{ \partial^2 u }{ \partial t^2 }=\sum_{n=1}^\infty u_{n}''(t)\sin(nx)$
$\frac{ \partial^2 u }{ \partial x^2 }=\sum_{n=1}^\infty -u_{n}(t)n^2\sin(nx)$
plug them into the equation
$\sum_{n=1}^\infty \underbrace{ \left( u_{n}''+n^2u_{n}+\frac{2t}{n}(-1)^n \right) }_{ =0 }\sin(nx)=0$
$u''_{n}+n^2u_{n}=\frac{2}{n}(-1)^{n+1}t, \quad n=1,2,\dots$
^Hey, we got a DE!
use method of undetermined coefficients #mouc (or laplace, but that'll take much longer.)
characteristic eq:
$r^2+n^2=0$
$r_{1,2}=\pm in$
homogenous solution is simply:
$u_{n}^h(t)=a_{n}\cos(nt)+b_{n}\sin(nt)$
particular solution is guessed in the form:
$u_{n}^p(t)=At+B$
$B=0$ because there's no constant term on the RHS
$A=\frac{2(-1)^{n+1}}{n^3}$
$u_{n}(t)=a_{n}\cos(nt)+b_{n}\sin(nt)+\frac{2(-1)^{n+1}}{n^3}t$
$u(x,t)=\sum_{n=1}^\infty(a_{n}\cos(nt)+b_{n}\sin(nt)+\frac{2(-1)^{n+1}}{n^3}t)\sin(nx)$
This is the last problem I'll be solving in my career. This is the last time he's teaching math 201 :( or any course for that matter.
$u(x,0)=\sum_{n=1}^\infty a_{n}\sin(nx)=\sin(x)$
$a_{1}=1, \quad a_{k}=0, \quad k=2,3,\dots$
$\frac{ \partial u }{ \partial t }(x,0)=\sum_{n=1}^\infty\left( b_{n}n+\frac{2(-1)^{n+1}}{n^3} \right)\sin(nx)=5\sin(2x)-3\sin(5x)$
coefficients=0 if $n\ne2,5$
$\implies b_{n}=\frac{2}{n^4}(-1)^n, \quad n\ne 2,5$
$b_{2}=\frac{5}{2}+\frac{2(-1)^2}{2^4}$
$b_{5}=-\frac{3}{5}+\frac{2(-1)^5}{5^4}$
$$u(x,t)=\cos(t)\sin(x)+\frac{5}{2}\sin(2t)\sin(2x)-\frac{3}{5}\sin(5t)\sin(5x)+2\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^3}\left( t-\frac{\sin(nt)}{n} \right)\sin(nx)$$
Here's a plot showing the behavior of the string (graphed up to 40 harmonics):
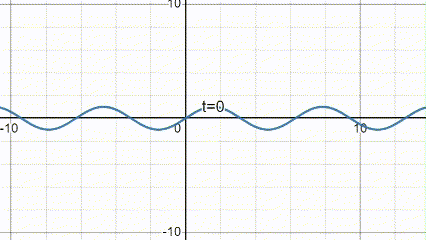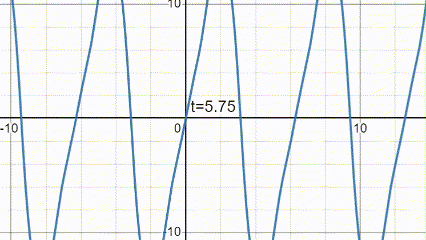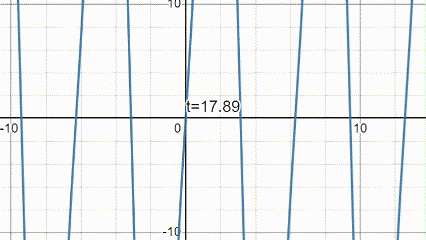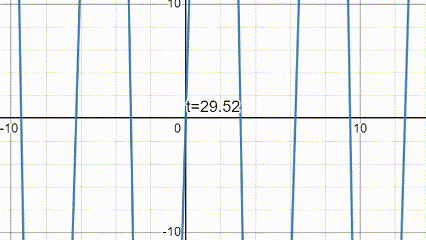
Finished the solution. Man I got teary eyed from this lecture.
#end of lec 35
#start of lec 36
# Last lecture
What do you guys wanna do? Questions or summary of the course?
Okay we do summary.
## Summary of second half of Math 201
(available on eclass)
Laplace transforms:
Definition of laplace,
Properties (4 important ones)
... (I decided to listen rather than note down.)
#end of lec 36
#end of Math 201. Congratulations!